Note: Woven Planet became Woven by Toyota on April 1, 2023.

[Fig.1]
By Takuya Ikeda (Senior Engineer) and Koichi Nishiwaki (Principal Robotics Researcher), in the Robotics Team of the Woven City Management Team
Smart cities have been a hot topic recently, and some of you may have heard of Woven City, a smart city that is being built in Susono, Shizuoka, Japan, as a big and bold project by Toyota Motor Corporation and Woven Planet Holdings, Inc. (Woven Planet). We are motivated by the audacious goal to elevate happiness for humankind, broadening our scope to include the everyday mobility of people, goods, and information, and are eager to pioneer a profound evolution in how societies of the future live, work, play, and move through the development of this innovative smart city. Curious to know how we are taking this challenge? We take an approach that is driven by three unwavering principles: “Human-Centered” respect and prioritization of people’s needs and preferences; “Living Laboratory” which enables seamless real-world testing of new technologies; and an “Ever-Evolving’’ approach by which such new technologies and services continuously grow and improve.
As robotics engineers, from the perspective of the everyday mobility of goods, we aim to help Woven City’s residents save time to enjoy their lives by giving them options such as providing them with a tidying up service. To realize such services, we believe the robotics that can acquire, sort, manipulate, and use household objects could be of assistance, and object pose estimation in indoor scenes is one such core technology, as shown in Fig.1.
Challenging Problems
The indoor environment is often cluttered as shown in Fig.2. In such an environment, there are several difficulties with estimating the target object pose precisely. One problem is occlusion. Occlusion often makes the estimation accuracy worse because a robot cannot see the full view of the target object. For example, as shown on the right side of Fig.2, it’s difficult to estimate the accurate pose of the red mug because the robot can only capture a tiny part of its appearance.

[Fig.2]
One Solution
How does a robot solve this problem? Let’s think about how a person would handle this problem. If you’re trying to manipulate this object precisely, you might move your head and eye to see the less-occluded object’s appearance from a different viewpoint. This is because we try to observe more reliable information based on uncertainty. We believe uncertainty is an important factor for robust object location and orientation (6D pose) estimation. So, we’d like to get the uncertainty of the estimated object pose and use it to estimate the object pose with low uncertainty.
For example, as shown in Fig.3, we can judge the reliability of the estimated result based on the uncertainty and we can obtain a more reliable result if we can fuse multiple information sources based on uncertainty.

[Fig. 3]
What is an ideal rotation representation with uncertainty?
Although pose can be disentangled to rotation and translation parts, ascertaining the ideal rotation representation with uncertainty is a controversial topic because of the SO(3) feature, for example, simple Gaussian distribution doesn’t fit to represent a 3D rotation group in contrast with a translation group.
So, we consider rotation representation which can represent uncertainty in this blog. While quaternion is a common choice for rotation representation of a 6D pose, it cannot represent the uncertainty of the observation. In order to handle the uncertainty of rotation, Bingham distribution is one promising form of representation because it has suitable features, such as the probability distribution, in addition to a smooth representation over SO(3). Bingham distribution is defined below:

The distribution can be parametrized by a 4D symmetric matrix, which is determined by 10 parameters.
Application
In recent years, a deep learning framework has been widely used for object pose estimation. So, we leverage Bingham distribution as a rotation representation for DNN-based 6D pose estimation. For more details, please see our paper.
As an application, we adapted our representation to an existing object pose estimator, which is PoseCNN. We can easily adapt our Bingham loss function to an existing pose estimation network utilizing quaternion representation as shown in Fig.4. Our representation can estimate object poses with ambiguity. If the network is trained correctly, we can know how reliable these results are based on the distribution.
[Fig.4]
For example, the large occlusion results in an output with large uncertainty as shown in Fig.5. So, we can utilize this distribution for the fusion of multiple information, outlier removal, etc.
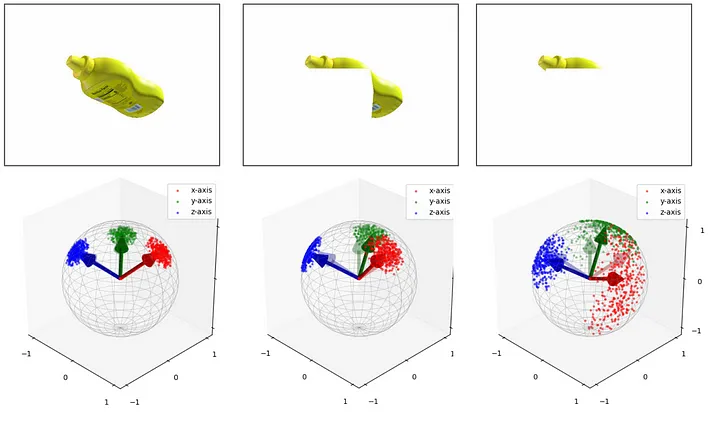
[Fig.5]
Conclusion
We introduced one promising rotation representation with uncertainty. As an application example, we also showed a 6D pose estimation network based on Bingham distribution.
In future work, we would like to manipulate household objects in a cluttered indoor scene based on this estimator.
Join us! 👋
Last year, an intern member worked with us on this and contributed a great deal. This year, we will continue to run the internship program and are looking forward to working with the new intern. Interested in joining us? Please check it out. We are also actively hiring exceptional talent for the robotics team. If you are interested in working with us in our office in Nihonbashi, Tokyo, please have a look at our current open positions!
Reference
Sato, Hiroya, Takuya Ikeda, and Koichi Nishiwaki. “Probabilistic Rotation Representation With an Efficiently Computable Bingham Loss Function and Its Application to Pose Estimation.” arXiv preprint arXiv:2203.04456 (2022).
Xiang, Yu, et al. “Posecnn: A convolutional neural network for 6d object pose estimation in cluttered scenes.” arXiv preprint arXiv:1711.00199 (2017).
Calli, Berk, et al. “Benchmarking in manipulation research: The YCB object and model set and benchmarking protocols.” arXiv preprint arXiv:1502.03143 (2015).